There are many ways to raise a mathematically competent child. It is important to know that. Children are individuals and there is no one formula that works for each child. However, I do believe that weaving math into their lives and making it a part of regular life helps. What I mean are children who are able to think on their feet about a mathematical situation, are comfortable asking questions, like talking about math, have their own ideas, and can work with others or independently to resolve math situations or problems. They should feel capable enough and find math interesting enough to enjoy it.



This is how it happened with our child. When Milena was about a year or two I was fortunate to have a day-long workshop with Professor Angela Andrews. I was in a school psychology graduate program and she was teaching us about developing early numeracy in children. This was around 2007, so I don’t remember everything she said, but I do remember that she said you should count with your child when you were doing things and just weave numbers in to develop their sense of numeracy. So, I believe that I became more conscious of counting aloud with my daughter, both forwards and backwards.
Numbers came up a lot when Milena was young. If she was eating dinner and she asked how much she had to eat of a certain vegetable like broccoli, when she was 3, I would say two-thirds or four-fifths. It was never a half, or the whole thing. Then she would move the food around on her plate, separating out the part she was going to eat from the part she would not, and I would look at it and I would judge to see if that was about right. It was not that I was telling her to count, or explaining any specific formula, but I was telling her when I did think it was about the fraction I was asking for, and she did get a visual sense of it being more than half. She also learned that fractions were less than the whole of the thing. This is an important idea as well. When we would walk places we might count our steps, and we would count backwards too. Walking backwards can be so much fun. We counted in German and English so we got a sense that numbers were not tied to a specific language, but it was an amount that could have different names.



When she was five she got an allowance. She got 6 quarters from me, and two from her father. So, that was 8 quarters. She could count them, and she knew that they made two dollars. We lived about a block from a toy store and she liked me to take her there. They had bins near the cash register of items that were around one to two dollars, like fun pencils or erasers, or little balls, or rings, or puzzles. They had all sorts of colorful and fun odds and ends. Soon, she got a good sense of all of the things in the store that were around three dollars and what was under ten dollars. This is an important sense of numeracy to develop, how much things cost. These were things she might save her money for in a couple of weeks. We also talked about tax. Our state has a sales tax that is about ten percent. So, I told her for each dollar that something costs, she has to add a dime for tax. So, she had to figure things out to see if she had enough money for the toys she wanted to buy, and I required her to do this in her head. Why? Because this is what people should be able to do when they are managing their money in a store. And, she was highly motivated to do it because she wanted to buy things to play with.




I once had a student who was not a very good math student except when it came to money. Why? His mother was home with several young children and she was not very organized. That meant that all day long she sent him, a sweet boy, to the store to buy things that she had forgotten to include the last time she sent him. She always sent him with cash. He was responsible for paying with cash, making sure that the change he got matched the receipt. That helped him to develop a good sense of money. It is money that helped Milena develop a good sense of numeracy. Milena has a good sense of what the things that she is interested in cost, which is very important. At one point we had been away for 3 weeks and she had not gotten any allowance. My husband gave her the 2 quarters per week that he owed her for allowance when we got back. So, she asked me “how many is 8 times 3?” I replied, “ 24.” She said, “then you owe me, “18 quarters.” It was the way that she set up the problem, knowing that I give her 6 quarters a week and that we were gone for 3 weeks. All are details she put together on her own, that made her come up with the correct amount of quarters that I owed her. That is conceptual competence.
My husband is a scientist and mathematician and we have a lot of conversations about mathematical ideas at dinner. Not exclusively, and not particularly about the math at school, but certainly about the math that comes up in life. Sometimes it is questions like discussing what infinity is like. We read the book The Number Devil by Hans Enzensberger to her when she was in third grade. She really enjoyed the story, which is in a well illustrated book about a boy who does not like math and has dreams that are plagued by a devil who is having to solve all sorts of numerical problems. These problems introduce one to interesting ideas in mathematics. I have read it to my third and fourth grade students, sometimes one day of the week, and we spend time going over the problems. We did this with our daughter as well. We also started The Parrot’s Theorem by Denis Guedj, which she and her father then continued reading on occasion. We lost interest in reading it at bedtime. It was perhaps too advanced, or too slow moving for us at the time. She was in third grade. It is a history of mathematical ideas woven into a story that has a man and a boy and a parrot. It has some illustrations, but more like a math text book than a picture book. There were other mathematical picture books, but these two stand out as the more substantive stories about mathematical ideas.
Milena also had the standard sorts of toys that would develop spatial sense. When she was about two she had building blocks, which had to be put away into a wooden case, and all could only fit just so. Those were the ones which were not colored. The older ones she inherited from me, which were all sorts of colors, so that the red rectangular ones were half of the blue rectangular blocks, and the small yellow ones were squares, where 2 yellows made a red and 4 yellows made a blue. Then, there were the orange triangular ones where two made a red, and 4 a blue, and the smaller green triangles where two made an orange or a yellow, in two different ways. They all could be used to build towers where tensile strength is also learned, as well as balance and shape and design. They could also be laid on the floor to make patterns. So many uses of the colored blocks. There were smaller pattern blocks and crayons, and pages to color in patterns which were enjoyed. We made many things with patterns. Here she was using geometry and fractions all the time as well as the physics of materials.
Later on my daughter became a miniature maker and worked with clay and paper to make items on a small scale. She taught others to make them too, so that they looked like the real thing only smaller. She was always in demand. This is using ratio. She also started making jewelry. Attractive jewelry requires a sense of pattern, with symmetry and asymmetry. My daughter also taught this to other people. She then went into beading. Beaded jewelry requires a lot of counting to get the pattern just right. It can be a pattern with different types of beads as well as with color. If you are making a multicolored pattern that changes shape you must count your beads, so that the triangle or circle works. A row that is off must be removed. A triangular pendant that is about one inch on each side can take many hours to make. Her beading masterpiece was a triangular shield she beaded as a symbol for the book Parzival, a Medieval German Epic poem or Novel-in-Verse by Wolfram von Eschenbach. It was a family crest, which took her at least 7 hours to bead. Unfortunately it was on display in school and was lost. The designing and creating were both mathematical and artistic. All of these artistic endeavors went into businesses that she developed. She also used these skills to help me with class fundraisers for global charities. The jewelry helped to raise enough money to help bring two families from Syria. In fact many thousands of dollars were raised. She donated her miniature making skills to a school fundraiser as well. She has developed such a good sense of how clays, papers, rubber bands, coins, beads, yarns, and other materials work, that she built the strongest bridge in the entire fourth grade and the best wind turbine in fifth grade. Her grade had 5 classes of around 23 students. This is why children have always benefitted from having time on their own to play around with their toys. Even taking them apart developed insights. Creating is not just play, it is building knowledge.

Whenever we go on family trips to Germany and are in my mother’s home city of Braunschweig, which is where the mathematician Gauss comes from, we see the mathematical formula he is credited with coming up with at the age of 8 or 9 painted on the glass of the windows of the SchlossArkaden, a mall next to the Braunschweiger Castle. Already, when my daughter was 8, and we were sitting at the table with family eating a meal, my husband would raise his glass in a toast and ask our daughter,” if everyone at this table toasts each person once how many toasts is that?” She would think for a moment and then come up with the correct answer. It is her ability to see this that makes me say she is mathematically competent. Her father would then ask her to explain how she knows that, and she would give a clear explanation. That has always been a strength of hers. She is able to give a clear explanation of her mathematical understanding.

In her first few years of school she did not have math every day. Sometimes 2 or 3 days a week. In the summer I taught her to add in her head by doubling single digit numbers first. Then adding the number one less would give you the sum one less, or adding one more would give you the sum one more. We did this with subtracting as well. Doubling taught her to multiply by 2s. So, she went into second grade knowing to add and subtract numbers up to 20 in her head and with pencil and paper up to one hundred. Her teacher taught her to tell time. Her third grade teacher had a problem of the day that my daughter liked to solve. She liked doing multiplication of double-digit numbers that year. Her fourth grade teacher had taught gifted math and had a wealth of interesting problems for children to solve. That was a great year. Milena had already identified herself in third grade as a math girl, which she felt was someone who likes to do interesting math. She has come to know herself as a mathematical learner. She prefers to have one very challenging problem that she would spend an hour or hours on, rather than a lot of basic problems that she just solves by applying a rote formula. Standardized tests were introduced in her school in third grade. I did not make much of a deal out of them. I just said that I always found them fun, which I did. We got our scores back when I was in school. Now-a-days, the school gives them to the parents, not the child. We also did not have them until fifth grade. Still, on the day of her first standardized test, she did not remember until we were right at the school, and then, with a little skip, she remembered she was taking them. Then, she went and took the test. She said that it was fun. Of course, these tests were untimed. That was the last time they were untimed. The following year they were not. It has not made a difference. However, by sixth grade she found them tedious because there were too many tests and it was just too long and they are after all, multiple choice tests. An American phenomenon. So, we have refused to have her take any preparation classes which many private school parents have had their children take or which her schools have offered. It does not seem fair to us that she is already in private school and then we pay for people to give her an additional edge. Of course, she does not need an edge. She will live with the scores she gets from the education she gets. While we want her to know the math that her school thinks she should know in each grade.
We want math to mostly be about solving interesting problems she likes, not getting a good score on a standardized test. That is learning for the sake of learning.
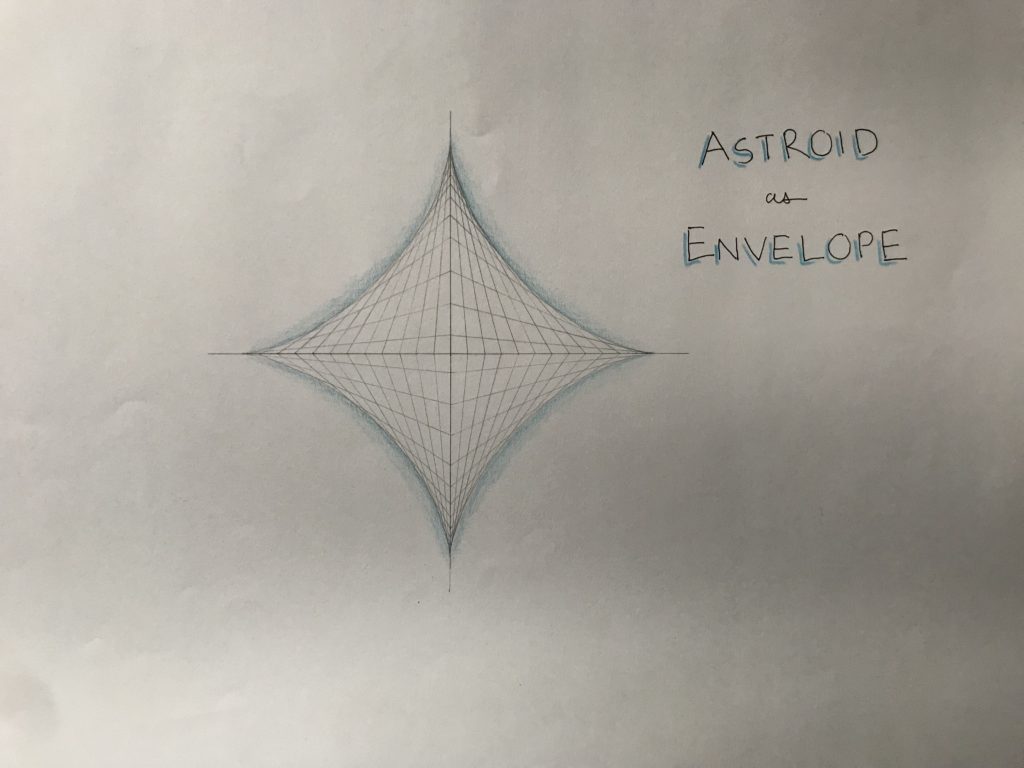
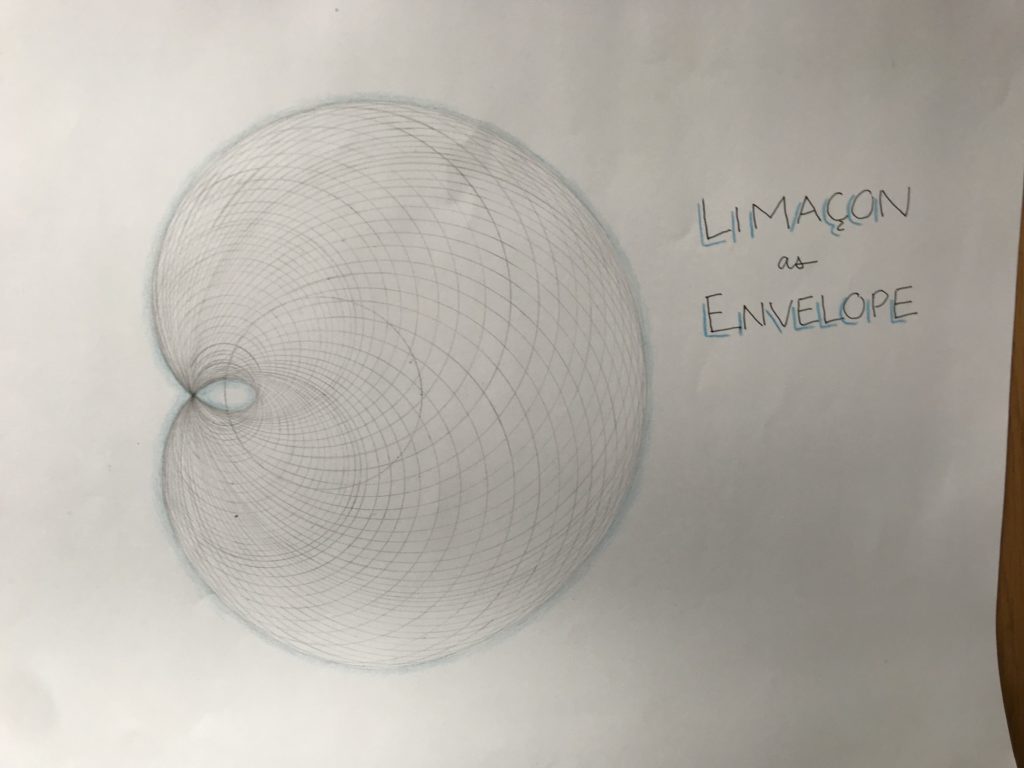
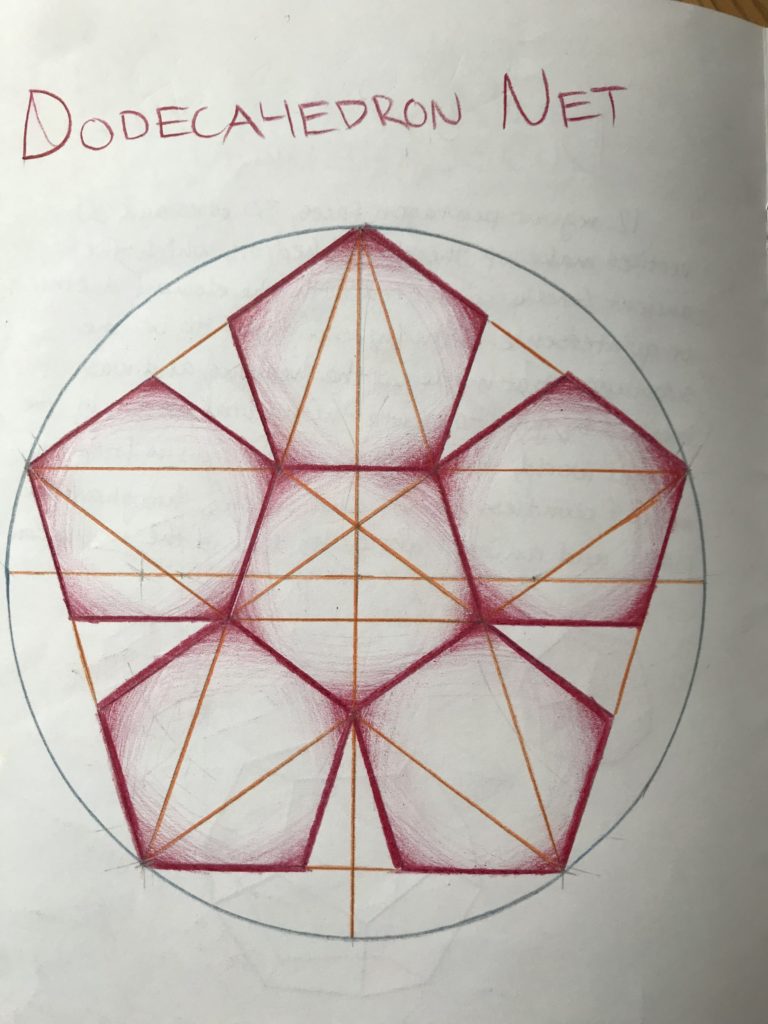
Her current school has not been a disappointment in this way. We have been very appreciative of the way that her high school approaches math instruction. Everyone can earn honors credit by doing the honors work and getting 80 percent of it correct, or done, or showing effort on solving it with good, clear explanations. Sometimes you can do honors problems instead of others less challenging problems. This can be in addition to the other work or instead of it depending on the task. The honors problems tend to be “challenge” problems and therefore interesting in the way that putting together a puzzle is interesting if you can do it. Sometimes our daughter might have to talk to someone to solve a puzzle, but mostly, she just wants to figure it out on her own. Milena also rarely has much math homework. This has been fine. If you can learn by understanding what is being explained and it makes sense that is great. Sometimes you need to try it out to be sure that you understand. In her sophomore year there was a Math Tea. This was where the children who participated explained “Challenge” problems that they had figured out to an audience, instead of being in a competition. It had a nice collegial feel. Like the only woman to win the Fields Medal in math, Maryam Mirzhakhani, whose mathematical work looked so much like visual art as she describes geometric and dynamic complexities of curved shapes, my daughter’s math classes have also had a lot of intricate geometric drawings. No Geometer’s Sketchpad or other computer aided drawing program for them. They are forming beautiful and carefully measured images of color by hand drawn lines. These are then displayed in the school, and turned into books. Something to keep and behold throughout life. So, math has had a romantic quality where they are invited to see its beauty too.
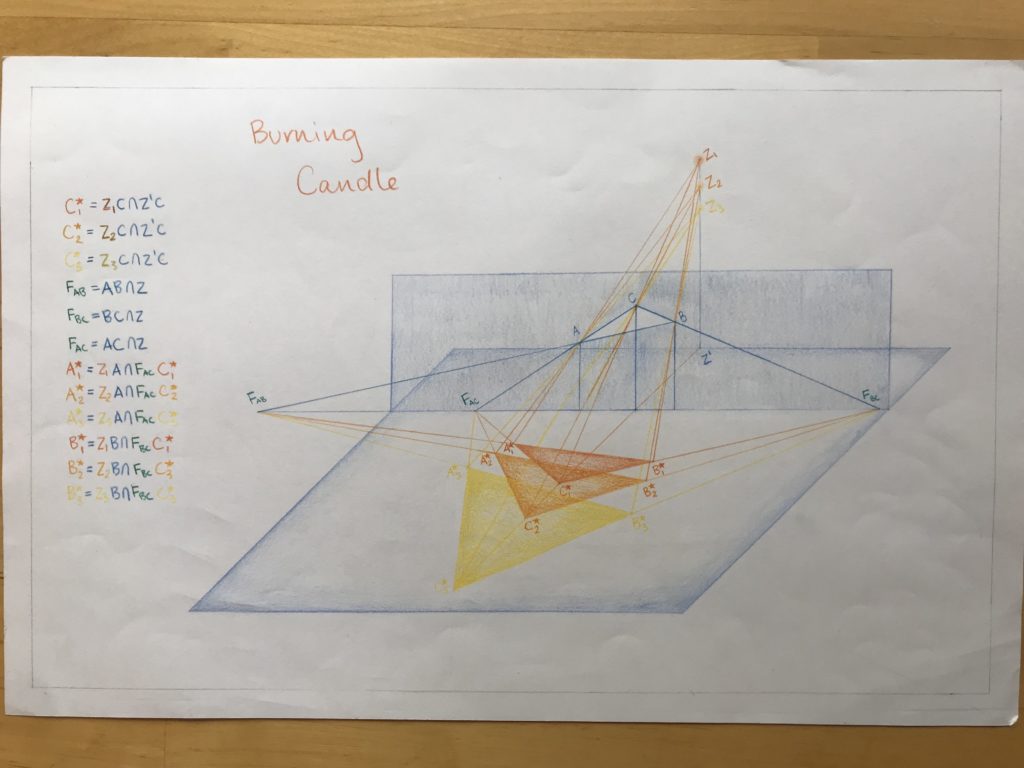
There are many other ways to raise a mathematically competent child. I know many children who win math competitions. Their parents have signed them up for all sorts of math courses, or spent a lot of time doing math with them. They enjoy math a lot because they are competent and because our society considers math ability to be an indicator of intelligence so they feel good about this recognition. That is what has worked for them. Milena enjoys being good at math, just as much as she enjoys the other subjects that she likes. Each has had its own time to shine in her life, and all are enjoyed when she is doing them. She does not have as many classmates now who like math as she did before in an earlier school where many children spent a lot of time taking extra math classes. I do think that math and reading are generally subjects that children should have over the summer because in the USA the summers are so long. One of her friends said to me in kind of an accusing tone one summer, that there were some parents who expected their children to read books, but I was the kind of parent who expects my child to read books and do math. I believe that my husband and I integrate math into our world in the way that we do reading. It is a part of life and sometimes the two even go together. In math and reading households, both belong. Math can be in making art and counting beads, or finding patterns, and they can be in a cooking class which is an art in itself, or designing, or a science class, or doing something creative with planting or building, or making anything. It might be solving a problem, or discussing an idea, like infinity and can there be more than one kind of infinity, or does something work. This is fair game for dinner conversation. A few years ago, the father of one of her friends told me that his daughter came home from our house and said that we had talked about math at the dinner table. Since my daughter’s friends have pointed this out, I assume that our conversations stand out as having math in them. To feel comfortable raising questions and discussing them is part of feeling mathematically comfortable and competent. In raising the math competent child, we have raised a child who is actually more than competent, she is engaged and sees math as a valid topic of discussion and inquiry as with other things. Math is also a means of playfulness. With play comes invention, and that is what we want to be encouraging. Our role as parents has been to some extent to protect this math love and playfulness and not let school take over and know better how it should be for our child. So, our formula has been to count with her, have math conversations, give her an allowance, provide our child with time and materials to explore her world, read books that include mathematical ideas, and support the types of math that she likes while making sure that she also knows the math she needs to know. Know your child, and what is good for them, and stand by them. That is how you will keep your child engaged and competent.

